题目内容
3.因式分解及其应用(1)4a2-64
(2)42.52+85×57.5+57.52(运用因式分解计算)
分析 (1)先提取公因式4,再对余下的多项式利用平方差公式继续分解.
(2)利用完全平方公式进行计算.
解答 解:(1)原式=4(a2-42)=4(a+4)(a-4);
(2)原式=42.52+2×42.5×57.5+57.52=(42.5+57.5)2=1002=10000.
点评 本题考查了因式分解的应用,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
14.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=k}\\{2x-y=8k}\end{array}\right.$的解也是二元一次方程3x+2y=10的解,则k的值为( )
| A. | 1 | B. | -2 | C. | 2 | D. | 4 |
11.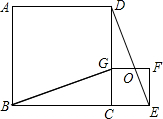 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列运算中,正确的是( )
| A. | $\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{(-2)×(-3)}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$ | C. | $\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2 | D. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ |
13.在下列4种正多边形的瓷砖图案中不能铺满地面的是( )
| A. |  | B. |  | C. |  | D. |  |
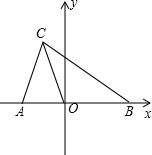 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.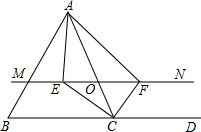 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.