题目内容
7.下列能用平方差公式计算的是( )| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(x+1) | D. | (2x+y)(2y-x) |
分析 这是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数.相乘的结果应该是:右边是乘式中两项的平方差(相同项的平方减去相反项的平方).
解答 解:A、应为(-x+y)(x-y)=-(x-y)(x-y)=-(x-y)2,故本选项错误;
B、(y-1)(-1-y)=-(x-1)(x+1)=-(x2-1),故本选项正确;
C、(x-2)(x+1)中只有相同项,没有没有互为相反数的项,不能利用平方差公式进行计算,故本选项错误;
D、(2x+y)(2y-x)中既没有相同的项,也没有互为相反数的项,不能利用平方差公式进行计算,故本选项错误.
故选:B.
点评 本题主要考查平方差公式:(1)两个两项式相乘;(2)有一项相同,另一项互为相反数,熟记公式结构是解题的关键.

练习册系列答案
相关题目
2.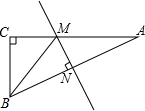 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )| A. | 18 | B. | 16 | C. | 17 | D. | 无法确定 |
12.下列运算中,正确的是( )
| A. | $\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{(-2)×(-3)}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$ | C. | $\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2 | D. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ |
16.一个多边形的每个内角均为108°,则这个多边形是( )边形.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
17.在下列长度的各组线段中,能构成直角三角形的是( )
| A. | 3,5,9 | B. | 4,6,8 | C. | 1,$\sqrt{3}$,2 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ |
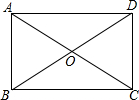 如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.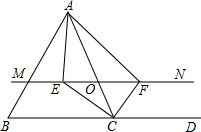 如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.
如图所示,△ABC中,点D在BC的延长线上,点O是AC边上的一个动点(不与A,C重合),过点O的直线MN∥BC,CE平分∠ACB交MN于点E,CF平分∠ACD交MN于点F.