题目内容
15.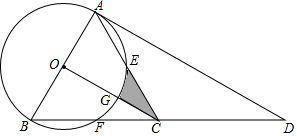 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F.
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F.(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=8,求线段CE、CG与GE围成的阴影部分的面积S.
分析 (1)欲证明AD是⊙O的切线,只要证明AD⊥AB即可;
(2)根据S阴=S△OEC-S扇形OEG,只要证明AE=EC,推出S△OEC=S△AOE=$\frac{\sqrt{3}}{4}$•42=4$\sqrt{3}$即可解决问题;
解答 (1)证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵CA=CD,
∴∠D=∠CAD,
∵∠ACB=∠D+∠CAD,
∴∠CAD=30°,
∴∠BAD=60°+30°=90°,
∴DA⊥BA,
∴AD是⊙O的切线.
(2)解:连接OE,
∵OA=OE,∠OAE=60°,
∴△OAE是等边三角形,
∴AE=AO=$\frac{1}{2}$AB=$\frac{1}{2}$AC,
∴AE=EC,
∴S△OEC=S△AOE=$\frac{\sqrt{3}}{4}$•42=4$\sqrt{3}$,
∵CA=CB,OA=OB,
∴CO⊥AB,
∴∠AOC=90°,
∴∠EOG=30°,
∴S扇形OEG=$\frac{30•π•{4}^{2}}{360}$=$\frac{4π}{3}$,
∴S阴=S△OEC-S扇形OEG=4$\sqrt{3}$-$\frac{4π}{3}$.
点评 本题考查切线的判定、等边三角形的性质、扇形的面积公式等知识,解题的关键是学会利用分割法求阴影部分面积,属于中考常考题型.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
5.下列运算中,正确的是( )
| A. | (x+y)2=x2+y2 | B. | x6÷x3=x2 | C. | -2(x-1)=-2x+2 | D. | 2-1=-2 |
6.下列各数:-0.101001,-3,$\sqrt{5}$,$\frac{22}{7}$,π,$\root{3}{6}$,0,$\root{3}{-1}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.有如下命题,其中错误的是( )
①负数没有立方根; ②一个实数的立方根不是正数就是负数;
③一个正数或负数的立方根与这个数同号; ④无理数不一定是无限小数.
①负数没有立方根; ②一个实数的立方根不是正数就是负数;
③一个正数或负数的立方根与这个数同号; ④无理数不一定是无限小数.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
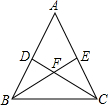 如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.
如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.


 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.