题目内容
 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论:
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论:①AD上任意一点到AB、AC的距离相等;②BD=CD;③S△ADB=S△ADC;④∠BDE=∠CDF
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:①根据角平分线性质即可判定;
②根据等腰三角形底边三线合一的性质即可解题;
③根据等腰三角形底边三线合一的性质即可解题;
④易证RT△BDE≌RT△CDF,即可解题.
②根据等腰三角形底边三线合一的性质即可解题;
③根据等腰三角形底边三线合一的性质即可解题;
④易证RT△BDE≌RT△CDF,即可解题.
解答:解:①∵AD是△ABC的角平分线,
∴AD上任意一点到AB、AC的距离相等,故①正确;
②∵AB=AC,AD是△ABC的角平分线,
∴点D是BC中点,
∴BD=CD,故②正确;
③∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∵BD=CD,
∴S△ADB=S△ADC,故③正确;
④∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在RT△BDE和RT△CDF中,
,
∴RT△BDE≌RT△CDF(HL),
∴∠BDE=∠CDF,故④正确;
故选 D.
∴AD上任意一点到AB、AC的距离相等,故①正确;
②∵AB=AC,AD是△ABC的角平分线,
∴点D是BC中点,
∴BD=CD,故②正确;
③∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∵BD=CD,
∴S△ADB=S△ADC,故③正确;
④∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在RT△BDE和RT△CDF中,
|
∴RT△BDE≌RT△CDF(HL),
∴∠BDE=∠CDF,故④正确;
故选 D.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,考查了等腰三角形底边三线合一的性质,本题中求证RT△BDE≌RT△CDF是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
在
,
,
,-
,3.
,3.1415,2.010101…(相邻两个1之间有1个0)中,无理数有( )
| 25 |
| 2 |
| 11 |
| 3 |
| π |
| 3 |
| •• |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 已知:如图,△ABC内接于圆,AB=AC,D为延长线上一点,AD交圆于E.求证:AB2=AD•AE.
已知:如图,△ABC内接于圆,AB=AC,D为延长线上一点,AD交圆于E.求证:AB2=AD•AE. 如图,东西方向的海岸线上有A、B两码头,相距100(
如图,东西方向的海岸线上有A、B两码头,相距100( 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.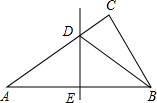 如图,在△ABC中,∠C=90°,DE垂直平分AB交AC于点D,垂足为E.
如图,在△ABC中,∠C=90°,DE垂直平分AB交AC于点D,垂足为E. 如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2
如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AB上一点O为圆心,AD为弦作⊙O.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AB上一点O为圆心,AD为弦作⊙O. 如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).
如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).