题目内容
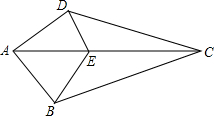 如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.
如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.考点:全等三角形的判定与性质
专题:
分析:易证△ACD≌△ACB,可得BC=CD,即可证明△DCE≌△BCE,可得∠DEC=∠BEC,即可解题.
解答:证明:在△ACD和△ACB中,
,
∴△ACD≌△ACB,(ASA)
∴BC=CD,
在△DCE和△BCE中,
,
∴△DCE≌△BCE(ASA),
∴∠DEC=∠BEC.
|
∴△ACD≌△ACB,(ASA)
∴BC=CD,
在△DCE和△BCE中,
|
∴△DCE≌△BCE(ASA),
∴∠DEC=∠BEC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△ACB和△DCE≌△BCE是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
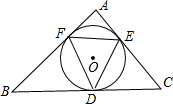 如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )
如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
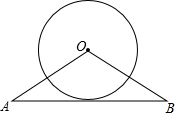 已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切.
已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切. 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论. 如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.
如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE. 如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2
如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2