题目内容
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )| A、50° | B、57.5° |
| C、60° | D、67.5° |
考点:切线的性质
专题:计算题
分析:根据切线的性质,由PD切⊙O于点C得到∠OCD=90°,再利互余计算出∠DOC=45°,加上∠A=∠ACO,∠COD=∠A+∠ACO,所以∠A=
∠COD=22.5°,然后根据三角形外角性质计算∠PCA的度数.
| 1 |
| 2 |
解答:解:∵PD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=45°,
∴∠DOC=90°-45°=45°,
∵OA=OC,
∴∠A=∠ACO,
∵∠COD=∠A+∠ACO,
∴∠A=
∠COD=22.5°,
∴∠PCA=∠A+∠D=22.5°+45°=67.5°.
故选D.
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=45°,
∴∠DOC=90°-45°=45°,
∵OA=OC,
∴∠A=∠ACO,
∵∠COD=∠A+∠ACO,
∴∠A=
| 1 |
| 2 |
∴∠PCA=∠A+∠D=22.5°+45°=67.5°.
故选D.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
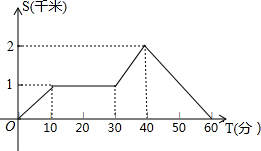 星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )
星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )| A、从家出发,休息一会,就回家 |
| B、从家出发,一直散步(没有停留),然后回家 |
| C、从家出发,休息一会,返回用时20分钟 |
| D、从家出发,休息一会,继续行走一段,然后回家 |
用科学记数法表示9 270 000正确的是( )
| A、9.27×106 |
| B、9.27×105 |
| C、9.27×104 |
| D、927×103 |
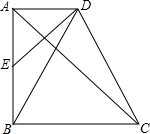 如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线
如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论. 如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2
如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AB上一点O为圆心,AD为弦作⊙O.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AB上一点O为圆心,AD为弦作⊙O. 如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).
如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).