题目内容
6.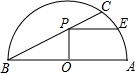 如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{5\sqrt{6}}{3}$ |
分析 连接OE,根据已知条件得到OB=OE=4,∠B=30°,根据三角函数的定义得到OP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,根据勾股定理即可得到结论.
解答  解:连接OE,
解:连接OE,
∵AB=4,
∴OB=OE=4,
∵$\widehat{AC}$的度数=60°,
∴∠B=30°,
∵OP⊥AB,
∴OP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,
∵PE∥AB,
∴OP⊥PE,
∴PE=$\sqrt{O{E}^{2}-O{P}^{2}}$=$\frac{4\sqrt{6}}{3}$,
故选C.
点评 本题考查了勾股定理,直角三角形的性质,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
19.某服装店公布以下好消息:为了感谢广大顾客的支持,即日起,在我店办会员卡同时享受以下两种优惠:
优惠一:
优惠二:
注:1-100是指购买服装的标价大于或等于1元且小于100元,其他类同.
若该店服装的标价都是正整数,请解决以下问题:
(1)在该店公布好消息的前、后,如果顾客都是充值1000元,在所买服装打折后的价格不超过会员卡内金额的前提下,可买到最贵的服装的标价相差了多少元?
(2)小红和小亮都在该店公布好消息之后办了会员卡,两人各买了一件标价高于300元的服装,小亮所买服装的标价比小红的高,但比较打折后的价格,小亮的低,求小亮买的服装的标价的范围.
优惠一:
| 充值金额(元) | 充值后卡内金额(元) | |
| 以前 | 即日起 | |
| 200 | 200 | 250 |
| 500 | 600 | 650 |
| 1000 | 1200 | 1400 |
| 购买服装的标价(元) | 折扣 | |
| 以前 | 即日起 | |
| 1-100 | 不打折 | 不打折 |
| 100-300 | 不打折 | 9折 |
| 300-400 | 9折 | 8折 |
| 不低于400 | 8折 | 7折 |
若该店服装的标价都是正整数,请解决以下问题:
(1)在该店公布好消息的前、后,如果顾客都是充值1000元,在所买服装打折后的价格不超过会员卡内金额的前提下,可买到最贵的服装的标价相差了多少元?
(2)小红和小亮都在该店公布好消息之后办了会员卡,两人各买了一件标价高于300元的服装,小亮所买服装的标价比小红的高,但比较打折后的价格,小亮的低,求小亮买的服装的标价的范围.
11. 如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )
如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )
 如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )
如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )| A. | $\frac{3+\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}+3\sqrt{2}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{5\sqrt{2}}{3}$ |
15.下面是教材第113页中,加权平均数的计算公式:$\overline{x}$=$\frac{{x}_{1}{f}_{1}+{x}_{2}{f}_{2}+{x}_{3}{f}_{3}+…+{x}_{k}{f}_{k}}{n}$,其中n表示的意义是( )
| A. | f1+f2+…+fk | B. | x1+x2+…+xk | C. | 1+2+…+k | D. | 以上都不对 |
16.已知a=-(0.5)2,b=-($\frac{1}{2}$)-2,c=(-$\frac{1}{2}$)-2,d=-(-0.2)0,比较a、b、c、d的大小结果为( )
| A. | c<a<b<d | B. | d<c<a<b | C. | a<b<c<d | D. | b<d<a<c |
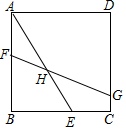 如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.
如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.