题目内容
18.已知⊙O是△ABD的外接圆,AB为直径,C为⊙O上一点,分别连接AC,CD,CD交AB于点P,AC=6,BD=7,CP=4,AP=3,则sin∠ADC=$\frac{18}{23}$.分析 根据相似三角形的性质得到PB=$\frac{14}{3}$,求得AB=$\frac{23}{3}$,连接BC,根据圆周角定理得到∠ABC=∠ADC,由AB是⊙O的直径,得到∠ACB=90°,根据三角函数的定义即可得到结论.
解答 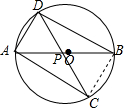 解:如图,∵∠CAB=∠CDB,∠ACD=∠ABD,
解:如图,∵∠CAB=∠CDB,∠ACD=∠ABD,
∴△APC∽△DPB,
∴$\frac{AC}{BD}=\frac{PC}{PB}$,
∵AC=6,BD=7,CP=4,
∴$\frac{6}{7}$=$\frac{4}{PB}$,
∴PB=$\frac{14}{3}$,
∴AB=$\frac{23}{3}$,
连接BC,则∠ABC=∠ADC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴sin∠ADC=sin∠ABC=$\frac{AC}{AB}$=$\frac{18}{23}$.
故答案为:$\frac{18}{23}$.
点评 本题考查了圆周角定理,相似三角形的判定和性质,三角函数的定义,正确的作出图形是解题的关键.

练习册系列答案
相关题目
6.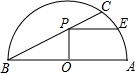 如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
 如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{5\sqrt{6}}{3}$ |
7.研究表明,某种动物体内的一种细胞直径约为0.000 00156m,用科学记数法表示是( )
| A. | 1.56×10-7 m | B. | 1.56×10-6m | C. | 1.56×10-8 m | D. | 1.56×10-9 m |
8.若-2a3b与5anbm+n是同类项,则mn的值是( )
| A. | -6 | B. | 8 | C. | -8 | D. | 6 |
 二次函数y=-x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第( )象限.
二次函数y=-x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第( )象限.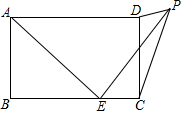 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.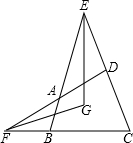 如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°.
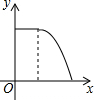
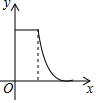
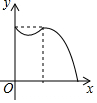
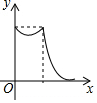
如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°.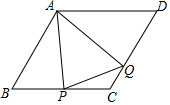 如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )