题目内容
1.已知x2+y2+6x+4y=-13,则yx的值为$-\frac{1}{8}$.分析 根据题目中的式子可以求得x、y的值,从而可以求得yx的值.
解答 解:∵x2+y2+6x+4y=-13,
∴x2+y2+6x+4y+13=0,
∴(x+3)2+(y+2)2=0,
∴x+3=0,y+2=0,
解得,x=-3,y-2,
∴yx=(-2)-3=$-\frac{1}{8}$,
故答案为:-$\frac{1}{8}$.
点评 本题考查配方法的应用、非负数的性质,解答本题的关键是明确题意,利用配方法和非负数的性质解答.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.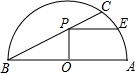 如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
 如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )
如图,点C是半圆O上一点,$\widehat{AC}$=60°,点P在弦BC上,且OP⊥AB于点O,过点P作PE∥AB交半圆O于点E,若AB=4,则PE的长为( )| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{5\sqrt{6}}{3}$ |
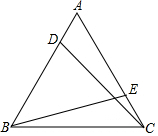 如图,在等边三角形ABC中,点D,E分别在边AB,AC上,且AD=CE,求证:CD=BE.
如图,在等边三角形ABC中,点D,E分别在边AB,AC上,且AD=CE,求证:CD=BE.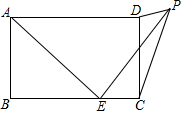 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.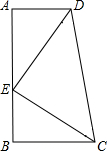 如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.
如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点. 如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )