题目内容
4. 甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图象可以得到:开始跑时,两人相距100m,则起跑时甲在乙前面100m,在50秒时甲,乙的距离是0,则起跑后50秒乙追上甲乙每50秒比甲多跑100m,所以经过25秒时甲乙相距50米.
解答 解:在50秒时甲,乙的距离是0,则起跑后50秒乙追上甲,故②说法正确;乙每50秒比甲多跑100m,所以经过25秒时甲乙相距50米,故③说法正确;乙每50秒比甲多跑100m,则在200秒时,相距300米.④说法不正确;乙的速度为1200/200=6m/s,故可以得出甲的速度为4m/s;故①正确.
故选C.
点评 主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
相关题目
13.有四根细木棒,长度分别为3cm,5cm,7cm,9cm,则随机抽出三根木棒,能够组成三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
14. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
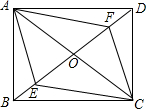 如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.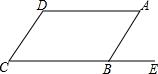 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.
如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.