题目内容
9.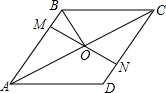 如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°.
如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°.
分析 根据菱形的判定与性质进而得出AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
解答 解:∵在?ABCD中,对角线AC平分∠BAD,
∴四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵$\left\{\begin{array}{l}{∠MAO=∠NCO}\\{AM=CN}\\{∠AMO=∠CNO}\end{array}\right.$,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°-28°=62°.
故答案为:62.
点评 本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )
| A. | 实际问题→收集数据→表示数据→整理数据→统计分析合理决策 | |
| B. | 实际问题→表示数据→收集数据→整理数据→统计分析合理决策 | |
| C. | 实际问题→收集数据→整理数据→表示数据→统计分析合理决策 | |
| D. | 实际问题→整理数据→收集数据→表示数据→统计分析合理决策 |
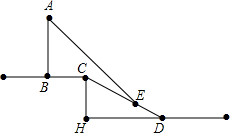 如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.

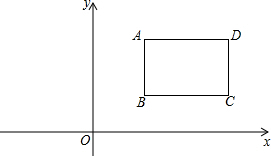 在平面直角坐标系和第一象限中有一矩形ABCD,AD平行于x轴,其中点A(3,4)且AB=2,BC=3.若将矩形ABCD向左平移a个单位之后,矩形到了第二象限,这时B、D两点在同一双曲线y=$\frac{k}{x}$上.
在平面直角坐标系和第一象限中有一矩形ABCD,AD平行于x轴,其中点A(3,4)且AB=2,BC=3.若将矩形ABCD向左平移a个单位之后,矩形到了第二象限,这时B、D两点在同一双曲线y=$\frac{k}{x}$上.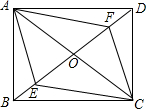 如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.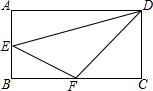 如图,在长方形ABCD中,AB=4cm,BC=8cm.E、F分别是AB、BC的中点.则E到DF的距离是3$\sqrt{2}$cm.
如图,在长方形ABCD中,AB=4cm,BC=8cm.E、F分别是AB、BC的中点.则E到DF的距离是3$\sqrt{2}$cm.