题目内容
19．
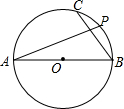如图，在⊙O中，AB是直径，BC是弦，点P是$\widehat{BC}$上任意一点．若AB=10，BC=6，则AP的长不可能是（ ）| A． | 6 | B． | 8 | C． | 9 | D． | 10 |
分析 首先连接AC，由圆周角定理可得，可得∠C=90°，继而求得AC的长，然后可求得AP的长的取值范围，继而求得答案
解答 解：连接AC，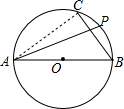
∵在⊙O中，AB是直径，
∴∠C=90°，
∵AB=10，BC=6，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8，
∵点P是$\widehat{BC}$上任意一点．
∴8≤AP≤10．
故选：A．
点评 此题考查了圆周角定理以及勾股定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
9．
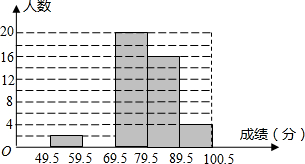某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数分布表和频数分布直方图：
请你根据图表提供的信息，解答下列问题：
（1）分布表中a=8，b=50，m=0.4，n=8%；
（2）补全频数直方图；
（3）如果80分以上为优秀，已知该年级共有学生600人，请你估计初一学生这次考试优秀的人数是多少？
某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数分布表和频数分布直方图：| 分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | b |
| 占调查总人数的百分比 | 4% | 16% | m | 32% | n | 1 |
（1）分布表中a=8，b=50，m=0.4，n=8%；
（2）补全频数直方图；
（3）如果80分以上为优秀，已知该年级共有学生600人，请你估计初一学生这次考试优秀的人数是多少？
10．
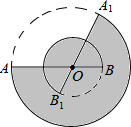O是线段AB上一点，OA=4，OB=2，线段AB绕O点逆时针方向旋转240°至线段A1B1，则图中阴影部分的面积是（ ）
O是线段AB上一点，OA=4，OB=2，线段AB绕O点逆时针方向旋转240°至线段A1B1，则图中阴影部分的面积是（ ）| A． | $\frac{16π}{3}$ | B． | 12π | C． | $\frac{32π}{3}$ | D． | $\frac{44π}{3}$ |
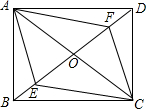如图，四边形ABCD的对角线AC，BD交于点O，已知O是BD的中点，BE=DF，AF∥CE．
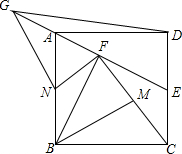正方形ABCD中，E为CD中点，BF⊥AE于F，M为CF上一点，将△BMF绕点F顺时针旋转得△GNF，M的对应点N点恰好在AB边上，B的对应点G恰好在线段EA的延长线上．若CM=$\frac{\sqrt{5}}{2}$，则DG的长为$\sqrt{10}$．
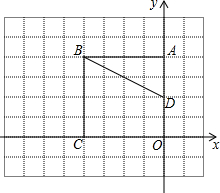如图，在直角坐标系中，A（0，4），B（-4，4），C（-4，0），D（0，2）．
8．若一次函数y=（m-7）x-2的图象经过第二、三、四象限，则m的取值范围是（ ）
| A． | m＞0 | B． | m＜0 | C． | m＞7 | D． | m＜7 |