题目内容
12.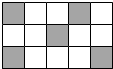 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
分析 首先确定在图中白色区域的面积在整个面积中占的比例,根据这个比例即可求出停在白色方砖上的概率.
解答 解:∵地面被等分成15份,其中白色部分占10份,
∴根据几何概率的意义,落在白色区域的概率=$\frac{10}{15}$=$\frac{2}{3}$.
故选:D.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用白色区域表示所求事件(A);然后计算白色区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
相关题目
3.已知三角形的两边长分别为8和4,则第三边长可能是( )
| A. | 3 | B. | 4 | C. | 8 | D. | 12 |
20.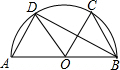 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
17.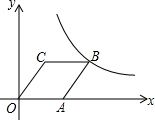 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
2.下列命题中,假命题的是( )
| A. | 同旁内角相等,两直线平行 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 同角(等角)的补角相等 | |
| D. | 三角形的一个外角大于任何一个与它不相邻的内角 |
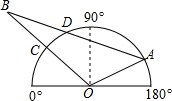 如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.
如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.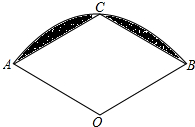 如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积.
如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积. 如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.
如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.