题目内容
1. 如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.
如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=20°,那么∠DCE的度数是25°.
分析 根据直角三角形的性质得到ED=EB=$\frac{1}{2}$AB,EC=$\frac{1}{2}$AB,等量代换得到ED=EC,根据等腰三角形的性质和三角形的外角的性质求出∠DEC=130°,计算即可.
解答 解:∵点E是Rt△ABD的斜边AB的中点,
∴ED=EB=$\frac{1}{2}$AB,
∴∠EDB=∠DBA=20°,
∴∠DEA=∠EDB+∠DBA=40°,
∵点E是Rt△ABC的斜边AB的中点,AC=BC,
∴EC=$\frac{1}{2}$AB,CE⊥AB,
∴∠DEC=130°,ED=EC,
∴∠DCE=25°,
故答案为:25°.
点评 本题考查的是直角三角形的性质和三角形的外角的性质以及等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
11. 如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
 如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )
如图,一个长为6.5米的梯子,一端放在离墙角2.5米处,另一端靠墙,则梯子顶端离墙角有( )| A. | 3米 | B. | 4米 | C. | 5米 | D. | 6米 |
12.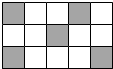 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
16.已知3x>-6y,则下列不等式不一定成立的是( )
| A. | $\frac{1}{2}$x>-y | B. | x+2>2-2y | C. | -x<2y | D. | $\frac{1}{x}>-\frac{1}{2y}$ |
13.小彭同时投掷两枚普通的正方体骰子(骰子各个面分别标有点数1,2,3,4,5,6),所得两个数字之和小于4的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
10.用同样大小的黑色棋子按如图所示的方式摆放图形,按照这样的规律摆下去,则第11个图形需棋子颗数为( )


| A. | 28 | B. | 31 | C. | 34 | D. | 37 |
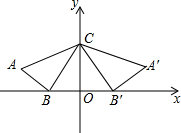 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-7,3),B(-3,0),C(0,4),将△ABC作关于y轴的轴对称图形得△A′B′C.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-7,3),B(-3,0),C(0,4),将△ABC作关于y轴的轴对称图形得△A′B′C.