题目内容
4.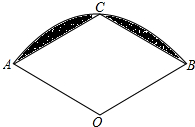 如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积.
如图,扇形AOB,半径OA=2,∠AOB=120°,C是弧AB的中点,连AC、BC,求图中阴影部分的面积.
分析 连接OC,过点A作AD⊥CD于点D,根据∠AOB=120°,C为弧AB的中点可知AC=BC,∠AOC=∠BOC=60°,故△ACO与△BOC为边长相等的两个等边三角形,再根据锐角三角函数的定义得出AD的长,由S阴影=S扇形AOB-2S△AOC即可得出结论.
解答 解:连接OC,过点A作AD⊥CD于点D,
∵∠AOB=120°,C为弧AB的中点,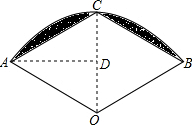
∴AC=BC,∠AOC=∠BOC=60°,
∴△ACO与△BOC为边长相等的两个等边三角形.
∵AO=2,
∴AD=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴S阴影=S扇形AOB-2S△AOC=$\frac{4π}{3}$-2$\sqrt{3}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
14.已知四组数据:①1.5,2,2.5;②3,4,5;③40,50,60;④$\frac{5}{4}$,1,$\frac{3}{4}$.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列事件是必然事件的是( )
| A. | 2016年两路镇房价一定下降 | |
| B. | 两个负数相乘,结果是正数 | |
| C. | 渝北区明天一定会下雪 | |
| D. | 小明努力学习,这次数学考试一定得满分 |
12.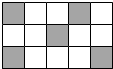 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
16.已知3x>-6y,则下列不等式不一定成立的是( )
| A. | $\frac{1}{2}$x>-y | B. | x+2>2-2y | C. | -x<2y | D. | $\frac{1}{x}>-\frac{1}{2y}$ |
13.小彭同时投掷两枚普通的正方体骰子(骰子各个面分别标有点数1,2,3,4,5,6),所得两个数字之和小于4的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |