题目内容
17.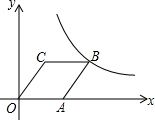 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 根据菱形的性质以及勾股定理得出AO=CO=2,即可得出B点坐标,进而求出k的值.
解答 解:∵菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,
∴CO=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴AO=BC=2,
∴B(3,$\sqrt{3}$),
∴k=xy=3×$\sqrt{3}$=3$\sqrt{3}$.
故选D.
点评 此题主要考查了菱形的性质以及勾股定理和反比例函数图象上点的坐标性质,得出B点坐标是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.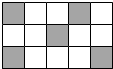 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
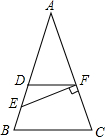 如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.
如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.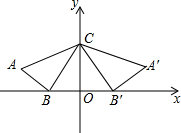 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-7,3),B(-3,0),C(0,4),将△ABC作关于y轴的轴对称图形得△A′B′C.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-7,3),B(-3,0),C(0,4),将△ABC作关于y轴的轴对称图形得△A′B′C.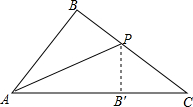 如图,△ABC中,AB=6,BC=8,AC=10,把△ABC沿AP折叠,使边AB与AC重合,点B落在AC边上的B′处,则折痕AP的长等于3$\sqrt{5}$.
如图,△ABC中,AB=6,BC=8,AC=10,把△ABC沿AP折叠,使边AB与AC重合,点B落在AC边上的B′处,则折痕AP的长等于3$\sqrt{5}$.