题目内容
15.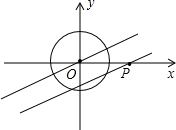 如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
分析 由题意得x有两个极值点,过点P与⊙O相切时,x取得极值,作出切线,利用切线的性质求解即可.
解答  解:将OA平移至P'D的位置,使P'D与圆相切,
解:将OA平移至P'D的位置,使P'D与圆相切,
连接OD,由题意得,OD=1,∠DOP'=30°,∠ODP'=90°,
故可得OP'=$\frac{OD}{cos30°}$=$\frac{2\sqrt{3}}{3}$,即x的极大值为$\frac{2\sqrt{3}}{3}$,
同理当点P在y轴左边时也有一个极值点,此时x取得极小值,x=-$\frac{2\sqrt{3}}{3}$,
综上可得x的范围为:-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$,
故答案为:-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了直线与圆的位置关系,分别得出两圆与圆相切时求出OP的长是解决问题的关键,难度一般,注意两个极值点的寻找.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
3.已知两个数的和是-7,积是6,则这两个数是( )
| A. | -4和-3 | B. | 4和3 | C. | 6和1 | D. | -6和-1 |
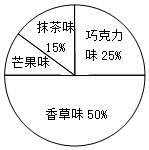 某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.如果知道香草口味冰淇淋一天售出200份,那么芒果口味冰淇淋一天售出的份数是( )
某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.如果知道香草口味冰淇淋一天售出200份,那么芒果口味冰淇淋一天售出的份数是( )