题目内容
6．如图1，将边长为a的大正方形剪去一个边长为b的小正方形（a＞b），将剩下的阴影部分沿图中的虚线剪开，拼接后得到图2，这种变化可以用含字母a，b的等式表示为a2-b2=（a+b）（a-b）．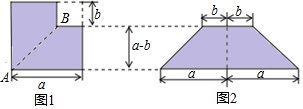
分析 根据左图中阴影部分的面积=大正方形的面积-小正方形的面积，或者右图中阴影部分的面积=梯形的面积，由面积不变可得公式．
解答 解：左图中阴影部分的面积=a2-b2，
右图中阴影部分的面积=$\frac{1}{2}$×（2a+2b）（a-b）=（a+b）（a-b）．
由图中阴影部分的面积不变，得a2-b2=（a+b）（a-b）．
故答案为：a2-b2=（a+b）（a-b）．
点评 本题主要考查平方差公式，注意运用数形结合的思想．
练习册系列答案
阅读快车系列答案
相关题目
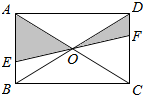如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，如果矩形的面积为1，那么阴影部分的面积是$\frac{1}{4}$．
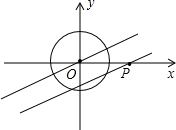如图，⊙O是以坐标原点为圆心，半径为1的圆，过点O的直线l与x轴的正半轴所夹锐角为30°，点P在x轴上运动，过点P且与直线l平行（或重合）的直线与⊙O有公共点，则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$．