题目内容
6.设α、β为方程2x2-$\sqrt{14}$x+1=0的两根,则(1)α2+β2=$\frac{5}{2}$;(2)(α-β)2=$\frac{3}{2}$;(3)($α+\frac{1}{β}$)($α-\frac{1}{β}$)=0.分析 根据根与系数的关系得到α+β=$\frac{\sqrt{14}}{2}$,αβ=$\frac{1}{2}$.
(1)将α2+β2变形为(α+β)2-2αβ,再整体代入计算即可求解;
(2)将)(α-β)2变形为(α+β)2-4αβ,再整体代入计算即可求解;
(3)先降次,将原式变形为$\frac{14αβ-\sqrt{14}(α+β)+1-1}{\sqrt{14}β-1}$,再整体代入分子计算即可求解.
解答 解:∵α、β为方程2x2-$\sqrt{14}$x+1=0的两根,
∴α+β=$\frac{\sqrt{14}}{2}$,αβ=$\frac{1}{2}$.
(1)α2+β2=(α+β)2-2αβ=($\frac{\sqrt{14}}{2}$)2-2×$\frac{1}{2}$=$\frac{5}{2}$;
(2)(α-β)2=α2+β2-2αβ=(α+β)2-4αβ=($\frac{\sqrt{14}}{2}$)2-4×$\frac{1}{2}$=$\frac{3}{2}$;
(3)($α+\frac{1}{β}$)($α-\frac{1}{β}$)=α2-$\frac{1}{{β}^{2}}$=$\sqrt{14}$α-1-$\frac{1}{\sqrt{14}β-1}$=$\frac{14αβ-\sqrt{14}(α+β)+1-1}{\sqrt{14}β-1}$=$\frac{7-\sqrt{14}×\frac{\sqrt{14}}{2}}{\sqrt{14}β-1}$=$\frac{7-7}{\sqrt{14}β-1}$=0.
故答案为:$\frac{5}{2}$;$\frac{3}{2}$;0.
点评 此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

①了解全班同学身高 ②了解CCTV1传统文化类节目《中国诗词大会》的收视率
③了解某班学生对“社会主义核心价值观”的知晓率 ④了解一批灯泡的使用寿命
适合采取全面调查的是( )
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
| 质量(g) | 73 | 74 | 75 | 76 | 77 | 78 |
| 甲的数量 | 2 | 4 | 4 | 3 | 1 | 1 |
| 乙的数量 | 2 | 3 | 6 | 2 | 1 | 1 |
(1)甲厂抽取质量的中位数是75g;乙厂抽取质量的众数是75g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数$\overline{x}$乙=75,方差S${\;}_{乙}^{2}$≈1.86.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
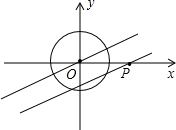 如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
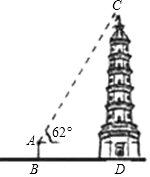 如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)