题目内容
10.如图是小棒摆成的图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…则第100个图案中有401根小木棒.
分析 依据数据5,9,13,再结合图形每次添加的部分为4根小棒,可得出每个图形所用小棒的根数与它当前是第几个图形之间的关系,代入数据,此题得解.
解答 解:∵第1个图案中有4+1=5根小棒,
第2个图案中有2×4+1=9根小棒,
第3个图案中有3×4+1=13根小棒,
…
∴第n个图案中有4n+1根小棒.
当n=100时,4n+1=401,
故答案为:401.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
20.我们已经学习过一次函数和反比例函数的图象和性质,类似地可以对函数y=x-$\frac{1}{x}$进行探索.下列结论:①图象在第一、三象限;②图象与y轴无交点;③图象与x轴只有一个交点;④图象关于原点成中心对称;⑤当x>0时,y随x的增大而增大;其中正确的结论是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②④⑤ | D. | ③④⑤ |
5.在函数y=$\frac{\sqrt{x+1}}{x-2}$中,自变量x的取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x≥-1且x≠2 | D. | x>-1且x≠2 |
1.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是75g;乙厂抽取质量的众数是75g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数$\overline{x}$乙=75,方差S${\;}_{乙}^{2}$≈1.86.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
| 质量(g) | 73 | 74 | 75 | 76 | 77 | 78 |
| 甲的数量 | 2 | 4 | 4 | 3 | 1 | 1 |
| 乙的数量 | 2 | 3 | 6 | 2 | 1 | 1 |
(1)甲厂抽取质量的中位数是75g;乙厂抽取质量的众数是75g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数$\overline{x}$乙=75,方差S${\;}_{乙}^{2}$≈1.86.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
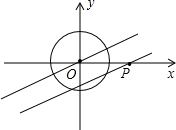 如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.
如图,⊙O是以坐标原点为圆心,半径为1的圆,过点O的直线l与x轴的正半轴所夹锐角为30°,点P在x轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标x的取值范围为-$\frac{2\sqrt{3}}{3}$≤x≤$\frac{2\sqrt{3}}{3}$.