题目内容
2.判断下列二次根式是否是最简二次根式,并说明理由.(1)$\sqrt{50}$;(2)$\sqrt{{a}^{2}bc}$;(3)$\sqrt{{x}^{2}+y}$;
(4)$\sqrt{0.75}$;(5)$\sqrt{(a+b)({a}^{2}-{b}^{2})}$;(6)$\frac{1}{2}$$\sqrt{6}$.
分析 根据最简二次根式的定义分别进行判断即可.
解答 解:(1)$\sqrt{50}$=5$\sqrt{2}$,不是最简二次根式;
(2)$\sqrt{{a}^{2}bc}$=|a|$\sqrt{bc}$,不是最简二次根式;
(3)$\sqrt{{x}^{2}+y}$是最简二次根式;
(4)$\sqrt{0.75}$=$\sqrt{\frac{3}{4}}$=$\frac{\sqrt{3}}{2}$,不是最简二次根式;
(5)$\sqrt{(a+b)({a}^{2}-{b}^{2})}$=$\sqrt{(a+b)(a+b)(a-b)}$=|a+b|$\sqrt{a-b}$,不是最简二次根式;
(6)$\frac{1}{2}$$\sqrt{6}$是最简二次根式.
点评 此题主要考查了最简二次根式的定义,满足下列两个条件的二次根式,叫做最简二次根式:(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含能开得尽方的因数或因式.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
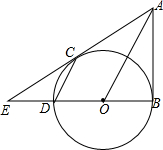 如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.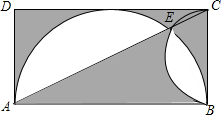 如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)
如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)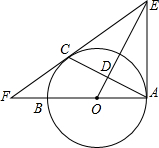 如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.
如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.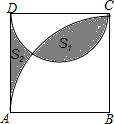 如图,正方形ABCD的边长为4,以CD为直径作半圆,以B为圆心,4为半径作圆弧,若图中阴影部分的面积分为S1、S2.则S1-S2=6π-16.(结果保留π)
如图,正方形ABCD的边长为4,以CD为直径作半圆,以B为圆心,4为半径作圆弧,若图中阴影部分的面积分为S1、S2.则S1-S2=6π-16.(结果保留π)