题目内容
13.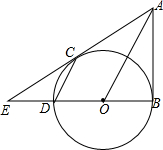 如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.
如图,过点A作⊙O的切线AB,AC,切点分别为B,C,直径BD的延长线与直线AC交于E,连接DC、OA.(1)求证:DC∥OA;
(2)若⊙O的半径为R.
①求DC•OA的值;
②当DC=R时,求sinE的值.
分析 (1)连接OC、BC,如图,先利用线段垂直平分线定理的逆定理得到OA垂直平分BC,再利用圆周角定理得到CD⊥BC,于是可判断CD∥OA;
(2)①证明Rt△AOB∽Rt△BDC,通过相似比可求出DC•OA的值;
②先判断△OCD为等边三角形得到∠COD=60°,再利用切线的性质得∠OCE=90°,则∠E=30°,然后利用特殊角的三角函数值值求解.
解答 (1)证明:连接OC、BC,如图,
∵AB、AC为⊙O的切线,
∴AB=AC,
而OB=OC,
∴OA垂直平分BC,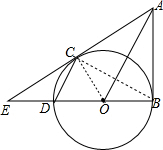
∵OB为直径,
∴∠BCD=90°,
∴CD⊥BC,
∴CD∥OA;
(2)解:①∵CD∥OA,
∴∠AOB=∠CDB,
∴Rt△AOB∽Rt△BDC,
∴$\frac{OA}{BD}$=$\frac{OB}{CD}$,
∴DC•OA=OB•BD=R•2R=2R2;
②∵DC=R,
∴DC=OC=OD,
∴△OCD为等边三角形,
∴∠COD=60°,
∵AE为切线,
∴OC⊥AE,
∴∠OCE=90°,
∴∠E=30°,
∴sinE=sin30°=$\frac{1}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决①小题的关键是证明△AOB∽Rt△BDC.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
3.据天津市统计局统计,2014年国庆黄金周七天长假,全市共接待游客755.52万人次,将755.52万用科学记数法表示应为( )人次.
| A. | 7.5552×102 | B. | 7.5552×103 | C. | 7.5552×106 | D. | 7.5552×107 |
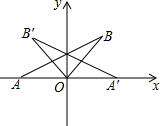 如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
如图,在△AOB中,OA=OB,∠AOB=135°,点A的坐标为(-1,0),△AOB与△A′OB′关于y轴对称,则点B′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).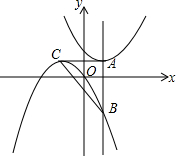 如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.
如图,在平面直角坐标系中,抛物线y=a(x-2)2+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x交于点B.抛物线y=-$\frac{1}{3}$x2-$\frac{4}{3}$x的顶点为C,连结CA、CB,则△ABC的面积为10.
 依据上述规律,
依据上述规律, ________.
________.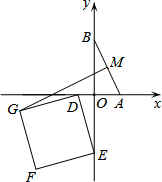 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为10+5$\sqrt{5}$.
在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为10+5$\sqrt{5}$.