题目内容
7.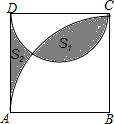 如图,正方形ABCD的边长为4,以CD为直径作半圆,以B为圆心,4为半径作圆弧,若图中阴影部分的面积分为S1、S2.则S1-S2=6π-16.(结果保留π)
如图,正方形ABCD的边长为4,以CD为直径作半圆,以B为圆心,4为半径作圆弧,若图中阴影部分的面积分为S1、S2.则S1-S2=6π-16.(结果保留π)
分析 观察图形可知,图中阴影部分的面积的差=半圆的面积+$\frac{1}{4}$圆的扇形面积-正方形面积,根据扇形的面积公式和正方形面积公式计算即可求解.
解答 解:S1-S2
=半圆的面积+$\frac{1}{4}$圆的扇形面积-正方形面积
=$\frac{1}{2}$π×(4÷2)2+$\frac{1}{4}$π×42-4×4
=2π+4π-16
=6π-16.
故答案为:6π-16.
点评 此题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.若x,y满足|x-1|+y2=6y-9,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 1 | B. | 3或5 | C. | 5或7 | D. | 7 |
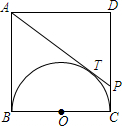 如图所示,O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的圆切于T点,求AT:AP的值.
如图所示,O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的圆切于T点,求AT:AP的值.