Question

6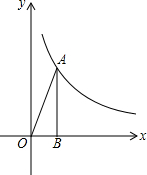．如图，点A（2，m）在双曲线y=$\frac{k}{x}$上，AB⊥x轴，B为垂足，tan∠AOB=2．
（1）求双曲线的解析式；
（2）P是AB右侧双曲线上的点，PC⊥x轴，C为垂足，若以P，B，C为顶点的三角形与△AOB相似，求点P的坐标．

Answer 1

分析 （1）根据点A（2，m），AB⊥x轴，tan∠AOB=2可得出OB及AB的长，故可得出A点坐标，代入反比例函数的解析式即可；
（2）设C（x，0），则P（x，$\frac{8}{x}$），再分△AOB∽△PBC与△AOB∽△BPC两种情况进行讨论．

解答 解：（1）∵点A（2，m），AB⊥x轴，tan∠AOB=2，
∴OB=2，AB=4，
∴A（2，4）．
∵点A（2，4）在双曲线y=$\frac{k}{x}$上，
∴k=2×4=8，
∴双曲线的解析式为y=$\frac{8}{x}$；

（2）设C（x，0），则P（x，$\frac{8}{x}$），
则一定有△AOB∽△PBC，
则$\frac{AB}{PC}$=$\frac{OB}{BC}$，即$\frac{4}{\frac{8}{x}}$=$\frac{2}{x-2}$，解得：x=1+$\sqrt{5}$或1-$\sqrt{5}$（舍去）
则P的坐标是（1+$\sqrt{5}$，2$\sqrt{5}$-2）；
当△AOB∽△BPC时，$\frac{AB}{BC}$=$\frac{OB}{PC}$，则$\frac{4}{x-2}$=$\frac{2}{\frac{8}{x}}$，解得：x=4或-2（舍去），
则P的坐标是（4，2）．
综上所述，符合条件的P点坐标为：P₁（1+$\sqrt{5}$，2$\sqrt{5}$-2），P₂（4，2）．

点评 本题考查的是反比例函数综合题，在解答此题时要注意进行分类讨论，不要漏解．