题目内容
8.解方程:$\frac{x}{x+3}$+$\frac{6}{{x}^{2}-9}$=$\frac{1}{x-3}$.分析 先把分式方程化为整式方程,再求出x的值,代入最减公分母进行检验即可.
解答 解:去分母得,x(x-3)+6=x+3,
去括号得,x2-3x+6=x+3,
移项,合并同类项得,x2-4x+3=0,解得x1=1,x2=3,
当x=1时,x2-9=1-9=-8≠0,故x=1是原方程的解;
当x=3时,x2-9=9-9=0,故x=3是原方程的增根.
综上可知,x=1是原分式方程的解.
点评 本题考查的是解分式方程,在解答此类题目时要注意进行验根.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD,若AB=3,AC=2.
如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD,若AB=3,AC=2.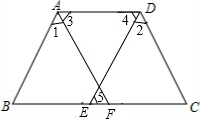 如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE.
如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE.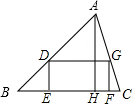 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M. 如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线交于点F,已知∠F=42°,则∠E=82度.
如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线交于点F,已知∠F=42°,则∠E=82度. 如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.