题目内容
 如图,过△ABC边BC上点D,作DE∥AC,DF∥AB,且∠ADE=∠ADF,求证:AD是△ABC的角平分线.
如图,过△ABC边BC上点D,作DE∥AC,DF∥AB,且∠ADE=∠ADF,求证:AD是△ABC的角平分线.考点:平行线的性质,三角形的角平分线、中线和高
专题:证明题
分析:根据平行线的性质,由DE∥AC得∠ADE=∠DAF,由DF∥AB得∠ADF=∠DAE,加上∠ADE=∠ADF,所以∠DAF=∠DAE,于是可判断AD是△ABC的角平分线.
解答:证明:∵DE∥AC,
∴∠ADE=∠DAF,
∵DF∥AB,
∴∠ADF=∠DAE,
而∠ADE=∠ADF,
∴∠DAF=∠DAE,
∴AD是△ABC的角平分线.
∴∠ADE=∠DAF,
∵DF∥AB,
∴∠ADF=∠DAE,
而∠ADE=∠ADF,
∴∠DAF=∠DAE,
∴AD是△ABC的角平分线.
点评:本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
 作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹)
作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹) 如图所示,四边形EFGH是四边形ABCD平移得到的.找出图中平行且相等的四条线段和一组全等的四边形.
如图所示,四边形EFGH是四边形ABCD平移得到的.找出图中平行且相等的四条线段和一组全等的四边形. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交EF于点F,BC=6.求CF的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交EF于点F,BC=6.求CF的长.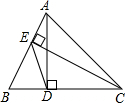 如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.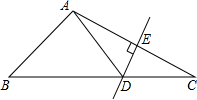 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,求△ABC的周长.
如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,求△ABC的周长. 如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若BC=10,则△AFE的周长为
如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若BC=10,则△AFE的周长为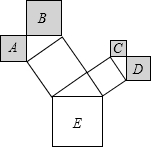 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是 已知,如图∠C=∠ABD=90°,AC=4,BC=3,AD=13,则求BD的长度.
已知,如图∠C=∠ABD=90°,AC=4,BC=3,AD=13,则求BD的长度.