题目内容
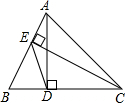 如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.考点:相似三角形的判定
专题:证明题
分析:根据垂直的定义得到∠ADB=90°,∠CEB=90°,则可根据圆周角定理得到点D和点E在以AC为直径的圆上,所以∠BDE=∠BAC,于是根据相似三角形的判定可判断△BDE∽△BAC.
解答:证明:∵AD⊥BC
∴∠ADB=90°
∵EC⊥AB
∴∠CEB=90°
∴点D和点E在以AC为直径的圆上,
∴∠BDE=∠BAC,
而∠DBE=∠ABC,
∴△BDE∽△BAC.
∴∠ADB=90°
∵EC⊥AB
∴∠CEB=90°
∴点D和点E在以AC为直径的圆上,
∴∠BDE=∠BAC,
而∠DBE=∠ABC,
∴△BDE∽△BAC.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了圆周角定理和圆内接四边形的性质.

练习册系列答案
相关题目
 已知a、b、c为有理数,且它们在数轴上的位置如图所示.
已知a、b、c为有理数,且它们在数轴上的位置如图所示. 如图,若圆心角∠AOB=110°,则圆周角∠ADB=
如图,若圆心角∠AOB=110°,则圆周角∠ADB= 在数轴上表示下列各数:0,1.5,3,
在数轴上表示下列各数:0,1.5,3,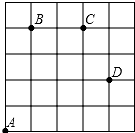 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向. 如图,过△ABC边BC上点D,作DE∥AC,DF∥AB,且∠ADE=∠ADF,求证:AD是△ABC的角平分线.
如图,过△ABC边BC上点D,作DE∥AC,DF∥AB,且∠ADE=∠ADF,求证:AD是△ABC的角平分线. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( ) 如图,求出下列直角三角形中未知边的长度.
如图,求出下列直角三角形中未知边的长度.