题目内容
5. 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成$△O{A_3}{B_{_3}}$,依此类推,已知A(1,3),A1(2,3),A2
(4,3),A3(8,3)…B(2,0),B1(4,0),B2
(8,0),B3(16,0)…
①观察每次变化后的三角形,找出规律,按此规律再将
△OA3B3变换成△OA4B4,则A4的坐标为(16,3),B4的坐标为(32,0)
②若按上述规律,将三角OAB进行n次变换,得三角形△OAnBn,比较每次变换三角形顶点的变化规律,探索顶点An的坐标为(2n,3),顶点Bn的坐标为(2n+1,0).
分析 根据图形写出点A系列的坐标与点B系列的坐标,根据具体数值找到规律即可.
解答 解:∵A(1,3),A1(2,3),A2(4,3),A3(8,3)…纵坐标不变为3,横坐标都和2有关,为2n,
∴An(2n,3);
∵B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,横坐标都和2有关为2n+1,
∴B的坐标为Bn(2n+1,0).
故答案为:①(16,3)(32,0)②(2n,3)(2n+1,0).
点评 此题考查点的坐标问题,依次观察各点的横纵坐标,得到规律是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.直角三角形两条直角边长为3cm和4cm,斜边上的高为( )
| A. | 3cm | B. | 2.4cm | C. | 2cm | D. | 3.6cm |
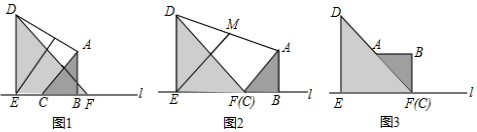
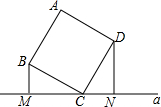 如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N
如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N 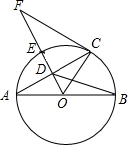 如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.
如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2. 有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)
有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)