题目内容
14.已知不等式组$\left\{\begin{array}{l}{x+1<a}\\{3x+5>x-7}\end{array}\right.$(1)若不等式组无解,求a的取值范围.
(2)若不等式组有解,求a的取值范围.
分析 (1)先求出两个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集即可;
(2)先求出两个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{x+1<a①}\\{3x+5>x-7②}\end{array}\right.$
∵解不等式①得:x<a-1,
解不等式②得:x>-6,
又∵不等式组无解,
∴a-1≤-6,
解得:a≤-5,
即a的取值范围是a≤-5;
(2)$\left\{\begin{array}{l}{x+1<a①}\\{3x+5>x-7②}\end{array}\right.$
∵解不等式①得:x<a-1,
解不等式②得:x>-6,
又∵不等式组有解,
∴a-1>-6,
解得:a>-5,
即a的取值范围是a>-5.
点评 本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是得出关于a的不等式,难度适中.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
6. 数轴上A点表示的数的倒数是( )
数轴上A点表示的数的倒数是( )
 数轴上A点表示的数的倒数是( )
数轴上A点表示的数的倒数是( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,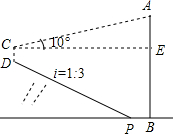 如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)
如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m) 如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.
如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.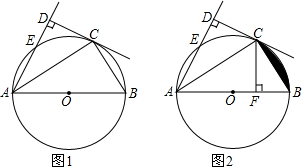
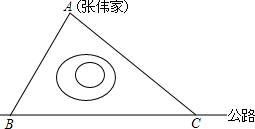 张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离.
张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离.