题目内容
17.在平面直角坐标系中,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为(0,1.5)或(0,-6).分析 分两种情况讨论:①当B′在x轴负半轴上时,过C作CD⊥AB于D,先求出A,B的坐标,分别为(3,0),(0,4),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=3,则DB=5-3=2,BC=4-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.②当B'在x轴正半轴上时,设OC=x,在Rt△OCB′中,利用勾股定理可求出x的值.
解答 解:①若B'在x轴左半轴,过C作CD⊥AB于D,如图1,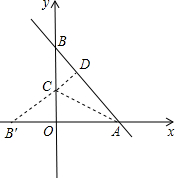
对于直线y=-$\frac{4}{3}$x+4,令x=0,得y=4;令y=0,x=3,
∴A(3,0),B(0,4),即OA=3,OB=4,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=4-n,
∴DA=OA=3,
∴DB=5-3=2,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+22=(4-n)2,解得n=1.5,
∴点C的坐标为(0,1.5).
②若B′在x轴右半轴,如图,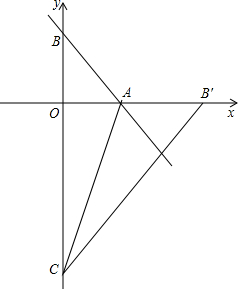
则AB′=AB=5,
设OC=x,则CB′=CB=x+4,OB′=OA+AB′=3+5=8,
在Rt△OCB′中,OB′2+OC2=CB′2,即82+x2=(x+4)2,
解得:x=6,即可得此时点C的坐标为(0,-6).
故答案为:(0,1.5)或(0,-6).
点评 本题考查了翻折变换的性质及求直线与坐标轴交点的坐标的方法:分别令x=0或y=0,求对应的y或x的值,也考查了勾股定理的应用,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 数轴上A点表示的数的倒数是( )
数轴上A点表示的数的倒数是( )
 数轴上A点表示的数的倒数是( )
数轴上A点表示的数的倒数是( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
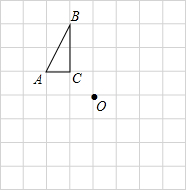 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形. 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,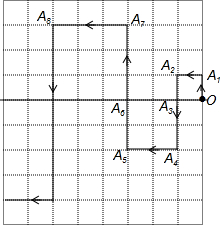 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示:
在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示: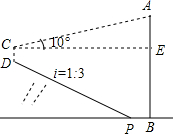 如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)
如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)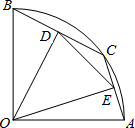 如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.
如图,在半径为4的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若四边形AOBC的面积为10,则△DOE的面积是$\frac{9}{2}$.