题目内容
15.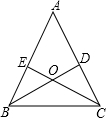 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
分析 欲证OB=OC,可证∠OBC=∠OCB,只要证明△BEC≌△CDB即可;由已知可得∠BEC=∠CDB=90°,∠ABC=∠ACB,BC是公共边,即可证得.
解答 证明:∵CE⊥AB,BD⊥AC,
∴∠BEC=∠CDB=90°,
在Rt△EBC与Rt△DCB中,
$\left\{\begin{array}{l}{∠BEC=∠CDB}\\{∠ABC=∠ACB}\\{BC=CB}\end{array}\right.$,
∴Rt△EBC≌Rt△DCB(AAS),
∴∠BCE=∠CBD,
∴OB=OC.
点评 本题主要考查了全等三角形的判定与性质,判定三角形全等是证明线段或角相等的重要方式,在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
7.将数据0.00000005464用科学记数法表示为( )
| A. | 5.464×10-7 | B. | 5.464×10-8 | C. | 5.464×10-9 | D. | 5.464×10-10 |
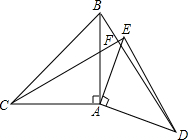 如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.
如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.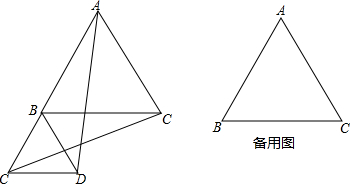
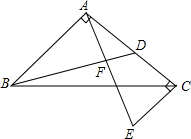 如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.
如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.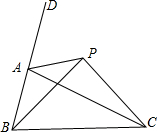 如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.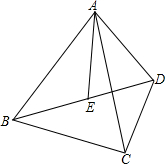 如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?
如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?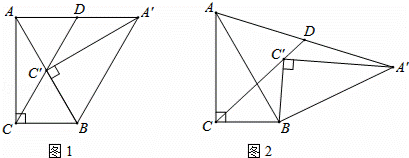
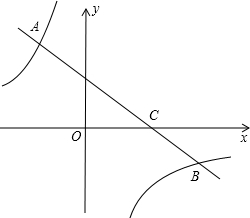 如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.