题目内容
5.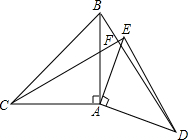 如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.
如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.(1)BD与CE具有怎样的位置关系和数量关系?并证明你的结论.
(2)当AC=2,∠BCE=15°时,求CF的长.
分析 (1)根据SAS即可求得△CAE≌△BAD,求得∠ACF=∠ABD.因为∠ANC=∠BNF,根据三角形的内角和定理就可求得∠BFN=∠NAC=90°,从而证得BD⊥CE;
(2)根据已知条件求得∠ACN=∠ACB-∠BCE=30°=∠FBN.在Rt△ACN中,通过解直角三角形从而求得AN=$\frac{2\sqrt{3}}{3}$.进而求得BN=2-$\frac{2\sqrt{3}}{3}$. 在Rt△ACN中通过解直角三角形求得NF=$\frac{1}{2}$.即可求得CF=CN+NF=1+$\sqrt{3}$.
解答 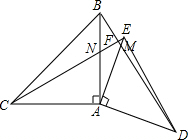 (1)证明:如图
(1)证明:如图
∵∠BAC=∠DAE=90°,∠BAE=∠BAE,
∴∠CAE=∠BAD,
在△CAE和△BAD中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$,
∴△CAE≌△BAD(SAS),
∴∠ACF=∠ABD,BD=CE
∵∠ANC=∠BNF,
∴∠BFN=∠NAC=90°,
∴BD⊥CE;
(2)∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°.
∵∠BCE=15°,
∴∠ACN=∠ACB-∠BCE=30°=∠FBN.
在Rt△ACN中
∵∠NAC=90°,AC=2,∠ACN=30°,
∴AN=$\frac{2\sqrt{3}}{3}$,CN=$\frac{4\sqrt{3}}{3}$,
∵AB=AC=2,
∴BN=2-$\frac{2\sqrt{3}}{3}$.
在Rt△ACN中
∵∠BFN=90°,∠FBN=30°,
∴NF=$\frac{1}{2}$BN=$\frac{3-\sqrt{3}}{3}$,
∴CF=CN+NF=1+$\sqrt{3}$.
点评 本题考查了等腰直角三角形的性质,全等三角形的判定,角的平分线的判定等知识点,利用全等三角形得出线段相等和角相等是解题的关键.

| A. | 甲需4天,乙需2天 | B. | 甲需3天,乙需1天 | C. | 甲需6天,乙需4天 | D. | 甲需5天,乙需3天 |
| A. | x1=2,x2=-1 | B. | x1=1,x2=-2 | C. | x1=3,x2=-2 | D. | x1=2,x2=-3 |
 如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.
如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.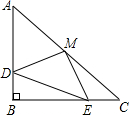 如图,已知△ABC中,∠B=90°,AB=BC,M为AC中点,BD=CE,判断△DME的形状.
如图,已知△ABC中,∠B=90°,AB=BC,M为AC中点,BD=CE,判断△DME的形状.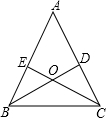 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.