题目内容
5.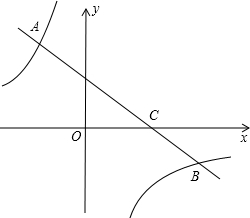 如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.(1)求该一次函数的解析式;
(2)若反比例函数y=$\frac{m}{x}$的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
分析 (1)先由一次函数y=kx+b(k<0)的图象经过点C(3,0),得出3k+b=0①,由于一次函数y=kx+b的图象与y轴的交点是(0,b),根据三角形的面积公式可求得b的值,然后利用待定系数法即可求得函数解析式;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.由△ACD∽△BCE,得出$\frac{AD}{BE}$=$\frac{AC}{BC}$=2,那么AD=2BE.设B点纵坐标为-n,则A点纵坐标为2n.由直线AB的解析式为y=-$\frac{2}{3}$x+2,得出A(3-3n,2n),B(3+$\frac{3}{2}$n,-n),再根据反比例函数y=$\frac{m}{x}$的图象经过A、B两点,列出方程(3-3n)•2n=(3+$\frac{3}{2}$n)•(-n),解方程求出n的值,那么m=(3-3n)•2n,代入计算即可.
解答 解:∵一次函数y=kx+b(k<0)的图象经过点C(3,0),
∴3k+b=0①,点C到y轴的距离是3,
∵k<0,
∴b>0,
∵一次函数y=kx+b的图象与y轴的交点是(0,b),
∴$\frac{1}{2}$×3×b=3,
解得:b=2.
把b=2代入①,解得:k=-$\frac{2}{3}$,则函数的解析式是y=-$\frac{2}{3}$x+2.
故这个函数的解析式为y=-$\frac{2}{3}$x+2;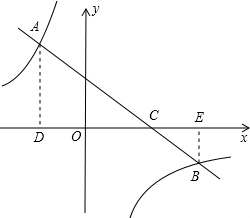 (2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.
(2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.
∵AD∥BE,
∴△ACD∽△BCE,
∴$\frac{AD}{BE}$=$\frac{AC}{BC}$=2,
∴AD=2BE.
设B点纵坐标为-n,则A点纵坐标为2n.
∵直线AB的解析式为y=-$\frac{2}{3}$x+2,
∴A(3-3n,2n),B(3+$\frac{3}{2}$n,-n),
∵反比例函数y=$\frac{m}{x}$的图象经过A、B两点,
∴(3-3n)•2n=(3+$\frac{3}{2}$n)•(-n),
解得n1=2,n2=0(不合题意舍去),
∴m=(3-3n)•2n=-3×4=-12.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积,相似三角形的判定与性质,一次函数、反比例函数图象上点的坐标特征,难度适中.正确求出一次函数的解析式是解题的关键.

| A. | x<-4或x>2 | B. | -4≤x≤2 | C. | x≤-4或x≥2 | D. | -4<x<2 |
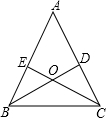 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.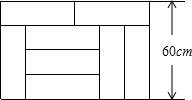 用二元一次方程组解决问题:
用二元一次方程组解决问题: 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.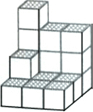 如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要19个小立方体,王亮所搭几何体的表面积为48.
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要19个小立方体,王亮所搭几何体的表面积为48.