题目内容
3.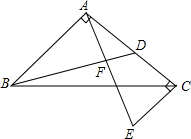 如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.
如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.
分析 先证出∠E=∠ADB,再由AAS证明△ACE≌△BAD,得出对应边相等即可.
解答 证明:∵AF⊥BD,CE⊥AC,
∴∠AFD=∠ACE=90°,
∴∠DAF+∠ADB=90°,∠DAF+∠E=90°,
∴∠E=∠ADB,
在△ACE和△BAD中,
$\left\{\begin{array}{l}{∠ACE=∠BAD=90°}&{\;}\\{∠E=∠ADB}&{\;}\\{AC=AB}&{\;}\end{array}\right.$,
∴△ACE≌△BAD(AAS),
∴AE=BD.
点评 本题考查了全等三角形的判定与性质、互余两角的关系;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.
如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.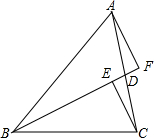 如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.
如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.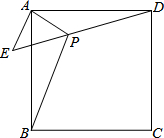 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.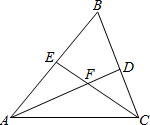 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.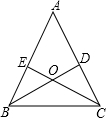 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC. 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.