题目内容
4.已知:Rt△ABC中,∠ACB=90°,∠ABC=60°,将Rt△ABC绕点B顺时针方向旋转α角(0°≤α≤120°),得到Rt△A′BC′,直线CC′和AA′相交于点D.(1)如图①,当点C′在AB边上时,判断线段AD和A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图①的位置旋转到图②的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图①的位置按顺时针方向旋转,当A、C′、A′三点在一条直线上时,请画出示意图,并写出旋转角的度数.
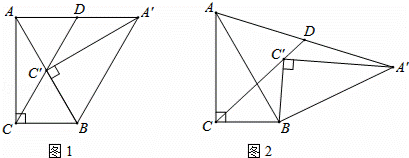
分析 (1)易证△BCC′和△BAA′都是等边三角形,从而可以求出∠AC′D=∠BAD=60°,∠DC′A′=∠DA′C′=30°,进而可以证到AD=DC′=A′D.
(2)解答中提供了两种方法,分别利用相似与全等,证明所得的结论.
(3)当A、C′、A′三点在一条直线上时,有∠AC′B=90°,易证Rt△ACB≌Rt△AC′B (HL),从而可以求出旋转角α的度数.
解答 解:(1)AD=A′D.
证明:如图1,
∵Rt△A′BC′≌Rt△ABC,
∴BC=BC′,BA=BA′,
∵∠A′BC′=∠ABC=60°,
∴△BCC′和△BAA′都是等边三角形,
∴∠BAA′=∠BC′C=60°,
∵∠A′C′B=90°,
∴∠DC′A′=30°,
∵∠AC′D=∠BC′C=60°,
∴∠ADC′=60°,
∴∠DA′C′=30°,
∴∠DAC′=∠DC′A,∠DC′A′=∠DA′C′,
∴AD=DC′,DC′=DA′,
∴AD=A′D;
(2)仍然成立:AD=A′D,
证法一:利用相似.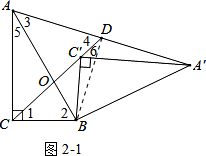 如图2-1:
如图2-1:
由旋转可得,BA=BA′,BC=BC′,∠CBC′=∠ABA′,
∵∠1=$\frac{1}{2}$(180°-∠ABA′),∠3=$\frac{1}{2}$(180°-∠CBC′),
∴∠1=∠3,
设AB、CD交于点O,则∠AOD=∠BOC,
∴△BOC∽△DOA,
∴∠2=∠4,$\frac{OB}{OD}$=$\frac{OC}{OA}$,
连接BD,
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴∠5=∠6,
∵∠ACB=90°,
∴∠2+∠5=90°,
∴∠4+∠6=90°,即∠ADB=90°,
∵BA=BA′,∠ADB=90°,
∴AD=A′D,
证法二:利用全等.如图2-2: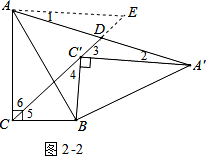
过点A作AE∥A′C′,交CD的延长线于点E,则∠1=∠2,∠E=∠3,
由旋转可得,AC=A′C′,BC=BC′,
∴∠4=∠5,
∵∠ACB=∠A′C′B=90°,
∴∠5+∠6=∠3+∠4=90°,
∴∠3=∠6,
∴∠E=∠6,∴AE=AC=A′C′,
在△ADE与△A′DC′中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AE=A′C′}\\{∠E=∠3}\end{array}\right.$,
∴△ADE≌△A′DC′(ASA),
∴AD=A′D;
(3)当A、C′、A′三点在一条直线上时,如图3,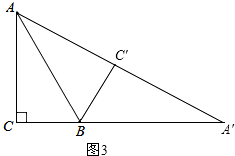
则有∠AC′B=180°-∠A′C′B=90°,
在Rt△ACB和Rt△AC′B中,
$\left\{\begin{array}{l}{BC=BC′}\\{AB=AB}\end{array}\right.$,
∴Rt△ACB≌Rt△AC′B (HL),
∴∠ABC=∠ABC′=60°,
∴当A、C′、A′三点在一条直线上时,旋转角α的度数为60°.
点评 本题考查了旋转的性质、等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质等知识,有一定的综合性.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案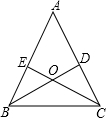 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.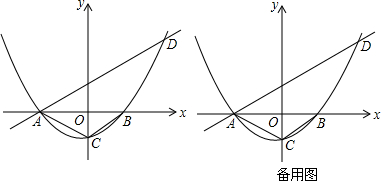
 用二元一次方程组解决问题:
用二元一次方程组解决问题: 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.