题目内容
10.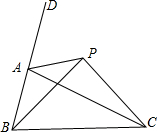 如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
分析 在BD上取一点E,使AE=AC,就可以得出△ACP≌△AEP,从而将四条不同的线段转化到一个三角形中进行求解,即可得出结论.
解答 解:PB+PC>AB+AC(2分)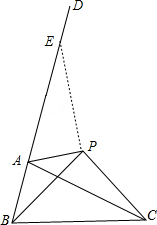
如图,在BD上取一点E,使AE=AC,连接EP.
∵AP是∠BAC的外角平分线,
∴∠CAP=∠EAP,
在△ACP和△AEP中,
$\left\{\begin{array}{l}{AC=AE}\\{∠CAP=∠EAP}\\{AP=AP}\end{array}\right.$,
∴△ACP≌△AEP(SAS),
∴PC=PE.
∵PB+PE>BE,
∴PB+PE>AB+AE,
∴PB+PE>AB+AC,
∴PB+PC>AB+AC.
点评 本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,三角形三边关系的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.为缓解甲、乙两地旱情,某水库计划向甲、乙两地送水,甲地需水量为180万立方米,乙地需电水量为120万立方米,现已两次送水:往甲地送水3天,乙地送水2天,共送水84万立方米;往甲地送水2天,乙地送水3天,共送水81万立方米,则完成往甲地,乙地送水任务还各需( )天.
| A. | 甲需4天,乙需2天 | B. | 甲需3天,乙需1天 | C. | 甲需6天,乙需4天 | D. | 甲需5天,乙需3天 |
20.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=-1,则使函数值y>0成立的x的取值范围是( )
| A. | x<-4或x>2 | B. | -4≤x≤2 | C. | x≤-4或x≥2 | D. | -4<x<2 |
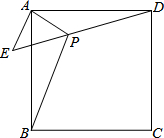 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.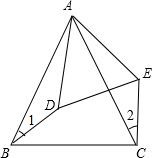 已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.
已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.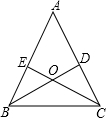 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
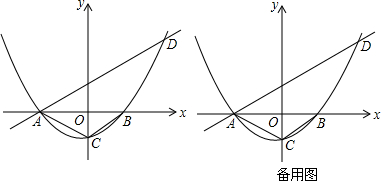
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.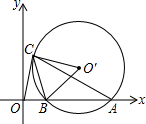 如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.
如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.