题目内容
20.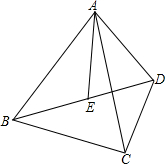 如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?
如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?
分析 由∠BAC=∠DAE根据等式的性质就可以得出∠BAE=∠CAD,就可以得出△BAE≌△CAD,就可以得出结论.
解答 解:BE=CD.
理由:∵∠BAC=∠DAE,
∴∠BAC-∠EAC=∠DAE-∠EAC,
∴∠BAE=∠CAD.
在△BAE和△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AD=AE}\end{array}\right.$,
∴△BAE≌△CAD(SAS),
∴BE=CD.
点评 本题考查了等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.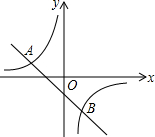 如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
 如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )| A. | -2<x<0或x>1 | B. | x<-2或x>1 | C. | x<-2或x>1 | D. | -2<x<1且x≠0 |
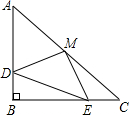 如图,已知△ABC中,∠B=90°,AB=BC,M为AC中点,BD=CE,判断△DME的形状.
如图,已知△ABC中,∠B=90°,AB=BC,M为AC中点,BD=CE,判断△DME的形状.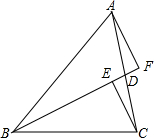 如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.
如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.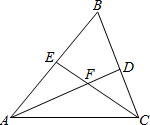 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.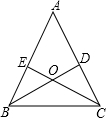 已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.
已知,如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且∠ABC=∠ACB,试说明OB=OC.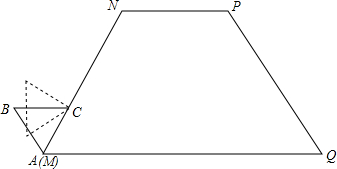
 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.