题目内容
13.用配方法解一元二次方程x2-6x+8=0时,则方程变形正确的是( )| A. | (x-3)2=17 | B. | (x+3)2=17 | C. | (x-3)2=1 | D. | (x+3)2=1 |
分析 首先把常数项移到等号右边,然后方程两边加上一次项系数的一半,配方即可.
解答 解:移项,得x2-6x=-8,
配方,x2-6x+9=1,
则(x-3)2=1.
故选C.
点评 本题考查了配方法解方程,用配方法解一元二次方程的步骤:①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.

练习册系列答案
相关题目
4.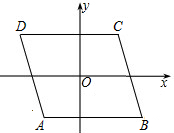 如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
 如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )| A. | (2,-3) | B. | (-2,3) | C. | (-3,-2) | D. | (-3,2) |
5. 如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
 如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )| A. | 72° | B. | 90° | C. | 108° | D. | 144° |
3.一元二次方程(3m+1)x2=2x的两根均为整数,则整数m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或1 |
 如图,在?ABCD中,BD是对角线,E,F分别为边AB,CD的中点.
如图,在?ABCD中,BD是对角线,E,F分别为边AB,CD的中点.