题目内容
7. “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )| A. | 30$\sqrt{3}$m | B. | 20$\sqrt{5}$m | C. | 30$\sqrt{2}$m | D. | 15$\sqrt{6}$m |
分析 过点D作DH垂直于AC,垂足为H,求出∠DAC的度数,判断出△BCD是等边三角形,再利用三角函数求出AB的长,从而得到AB+BC+CD的长.
解答 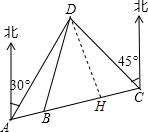 解:过点D作DH垂直于AC,垂足为H,
解:过点D作DH垂直于AC,垂足为H,
由题意可知∠DAC=75°-30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=30m,
∴DH=$\frac{\sqrt{3}}{2}$×30=15$\sqrt{3}$,
∴AD=$\sqrt{2}$DH=15$\sqrt{6}$m.
答:从A地到D地的距离是15$\sqrt{6}$m.
故选D.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
19.二次三项式3x2-2x-6的值为3,则x2-$\frac{2}{3}$x+6的值为( )
| A. | 18 | B. | 12 | C. | 9 | D. | 7 |
15.从标有号数1到100的100张卡片中,随意抽取一张,其号数为3的倍数的概率是( )
| A. | $\frac{33}{100}$ | B. | $\frac{34}{100}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
19.下列命题中真命题的有( )
①同位角相等;②在△ABC中,若∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
①同位角相等;②在△ABC中,若∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.在某班组织的跳绳比赛中,第一小组五位同学跳绳次数分别为198,230,220,216,209,则这五个数据的中位数为( )
| A. | 220 | B. | 218 | C. | 216 | D. | 209 |