题目内容
17.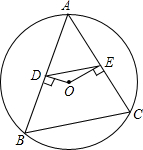 如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
分析 根据垂径定理得AD=BD,AE=CE,所以由三角形中位线定理得到:BC=2DE=6.
解答 解:∵OD⊥AB,
∴AD=DB,
∵OE⊥AC,
∴AE=CE,
∴DE为△ABC的中位线,
∴DE=$\frac{1}{2}$BC,
∴BC=2DE=2×3=6.
故答案是:6.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了三角形中位线定理.

练习册系列答案
相关题目
8.下列式子中与2ab2是同类项的是( )
| A. | 3ab | B. | 2b2 | C. | ab2 | D. | a2b |
12. 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )
 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠4 | D. | ∠5=∠1+∠3 |
9.在同一直角坐标系中,函数y=$-\frac{2}{x}$与y=2x图象的交点个数为( )
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
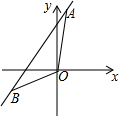 如图,直线a经过点A(1,6),和点B(-3,-2).
如图,直线a经过点A(1,6),和点B(-3,-2). 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.