题目内容
2.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表.关于这10户家庭的月用电量说法正确的是( )| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 4 | 2 | 2 | 1 |
| A. | 平均数是38.5 | B. | 众数是4 | C. | 中位数是40 | D. | 极差是3 |
分析 根据加权平均数、众数、中位数、极差的定义和计算公式分别对每一项进行分析,即可得出答案.
解答 解:A、这组数据的平均数(25+30×4+40×2+50×2+60)÷10=38.5,故本选项正确;
B、30出现的次数最多,出现了4次,则众数是30,故本选项错误;
C、把这些数从小到大排列,最中间两个数的平均数是(30+40)÷2=35,则中位数是35,故本选项错误;
D、这组数据的极差是:60-25=35,故本选项错误;
故选:A.
点评 此题考查了加权平均数、众数、中位数和极差,掌握中位数、众数、加权平均数和极差的定义和计算公式是本题的关键;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数;众数是一组数据中出现次数最多的数;求极差的方法是用一组数据中的最大值减去最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在Rt△ABC中,∠ACB=90°,AC=CB,CD是斜边AB的中线,若AB=2$\sqrt{2}$,则点D到BC的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{\sqrt{2}}{2}$ |
10.在平面直角坐标系中,点M(6,-3)关于x轴对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.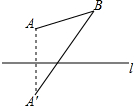 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )| A. | A′B2-AB2=13 | B. | A′B2-AB2=24 | C. | A′B2+AB2=25 | D. | A′B2+AB2=26 |
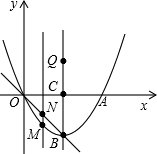 如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).