题目内容
11.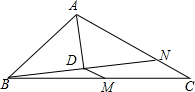 如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.
如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.
分析 根据等腰三角形三线合一的性质可得BD=DN,AB=AN,再求出CN,然后判断出DM是△BCN的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半解答.
解答 解:∵AD为∠BAC的平分线,BD⊥AD,
∴BD=DN,AB=AN=12,
∴CN=AC-AN=18-12=6,
又∵M为△ABC的边BC的中点
∴DM是△BCN的中位线,
∴MD=$\frac{1}{2}$CN=$\frac{1}{2}$×6=3,
故答案为:3.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形三线合一的性质,熟记定理与性质并作辅助线构造出以MD为中位线的三角形是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.化简:$\sqrt{-\frac{1}{a}}$=( )
| A. | $\frac{1}{a}$$\sqrt{a}$ | B. | $\frac{1}{a}$$\sqrt{-a}$ | C. | -$\frac{1}{a}$$\sqrt{-a}$ | D. | -$\frac{1}{a}$$\sqrt{a}$ |
2.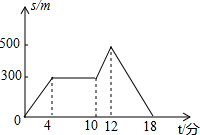 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )| A. | 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 | |
| B. | 从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 | |
| C. | 从家出发,一直散步(没有停留),然后回家了 | |
| D. | 从家出发,散了一会儿步,就找同学去了,18min后才开始返回 |
19.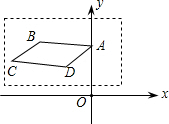 在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
 在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )| A. | 先向右平移5个单位,再向下平移1个单位 | |
| B. | 先向右平移5个单位,再向下平移3个单位 | |
| C. | 先向右平移4个单位,再向下平移4个单位 | |
| D. | 先向右平移4个单位,再向下平移3个单位 |
 如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )
如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )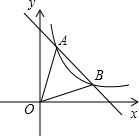 如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点,
如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点, 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).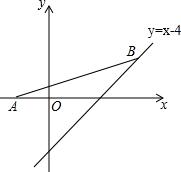 如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).
如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).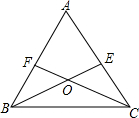 已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.
已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.