题目内容
20.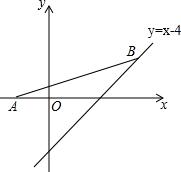 如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).
如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).
分析 过点A作AB′⊥已知直线,垂足为B′,设直线AB′的解析式为y=-x+b,将x=-2,y=0代入得;2+b=0,解得b=-2,从而得到AB′的解析式,然后将两直线的解析式组成方程组求解即可.
解答 解:过点A作AB′⊥已知直线,垂足为B′.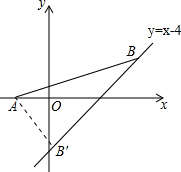
设直线AB′的解析式为y=-x+b,将x=-2,y=0代入得;2+b=0,解得b=-2,
∴直线AB′的解析式为y=-x-2,
将y=x-4与y=-x-2组成方程组得:$\left\{\begin{array}{l}{y=x-4}\\{y=-x-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$
∴点B′的坐标为(1,-3)即当线段AB最短时,点B坐标为(1,-3).
点评 本题主要考查的一次函数的应用,明确两条直线y1=k1x+b1与y2=k2x+b2相互垂直时k1k2=-1是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
10.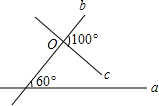 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
8.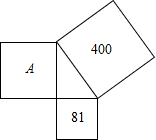 如图,三个正方形围成一个直角三角形,81、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是( )
如图,三个正方形围成一个直角三角形,81、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是( )
 如图,三个正方形围成一个直角三角形,81、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是( )
如图,三个正方形围成一个直角三角形,81、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是( )| A. | 11 | B. | 31 | C. | 319 | D. | 以上答案都不对 |
10.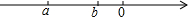 a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
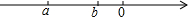 a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )| A. | G>H>M>N | B. | G>N>M>H | C. | G>M>N>H | D. | G>N>H>M |
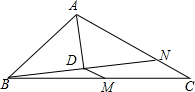 如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.
如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.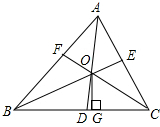 如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.
如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.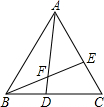 如图所示,△ABC为等边三角形,D、E分别是边BC、CA上的点,且有BD=CE,AD与BE交于点F.若AD=3,则BE的长为3.
如图所示,△ABC为等边三角形,D、E分别是边BC、CA上的点,且有BD=CE,AD与BE交于点F.若AD=3,则BE的长为3.