题目内容
1.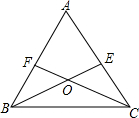 已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.
已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.
分析 连接OA,由三角形内角和定理和角平分线的定义得出∠OBC+∠OCB=60°,OA平分∠BAC,再由∠A+∠EOF=180°,得出点A、E、O、F四点共圆,得出$\widehat{OE}=\widehat{OF}$,即可得出结论.
解答 证明:连接OA,如图所示: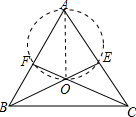
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE平分∠ABC,CF平分∠ACB,.
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,OA平分∠BAC,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°,∠EAO=∠FAO=30°,
∴∠EOF=∠BOC=180°-60°=120°,
∴∠A+∠EOF=180°,
∴点A、E、O、F四点共圆,
∵∠EAO=∠FAO,
∴$\widehat{OE}=\widehat{OF}$,
∴OE=OF.
点评 本题考查了角平分线的性质、三角形内角和定理、四点共圆、圆周角定理等知识;熟练掌握角平分线的性质,证明四点共圆是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.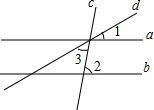 如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
 如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )| A. | 30° | B. | 40° | C. | 45° | D. | 75° |
13.多项式-a(a-x)(x-b)+ab(a-x)(b-x)的公因式是( )
| A. | -a | B. | -a(a-x)(x-b) | C. | a(a-x) | D. | -a(x-a) |
10.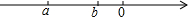 a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
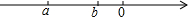 a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )
a,b两数在数轴上的位置如图所示,M=a+b,N=-a+b,H=a-b,G=-a-b,则下列正确的是( )| A. | G>H>M>N | B. | G>N>M>H | C. | G>M>N>H | D. | G>N>H>M |
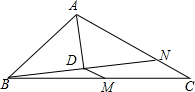 如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.
如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3. 如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为(0,-$\frac{9}{4}$).
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为(0,-$\frac{9}{4}$).