题目内容
6. 如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )
如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )| A. | 5° | B. | 10° | C. | 20° | D. | 30° |
分析 连接AH,CH,根据在四边形ABCD中,∠BCD=∠BAD=90°,H是BD的中点可知AH=CH=$\frac{1}{2}$BD,再由点G时AC的中点可知HG是线段AC的垂直平分线,故∠EGH=90°,再由对顶角相等可知∠GEH=∠BEC=80°,由直角三角形的性质即可得出结论.
解答 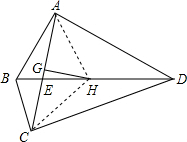 解:连接AH,CH,
解:连接AH,CH,
∵在四边形ABCD中,∠BCD=∠BAD=90°,H是BD的中点,
∴AH=CH=$\frac{1}{2}$BD.
∵点G时AC的中点,
∴HG是线段AC的垂直平分线,
∴∠EGH=90°.
∵∠BEC=80°,
∴∠GEH=∠BEC=80°,
∴∠GHE=90°-80°=10°.
故选B.
点评 本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解答此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
1.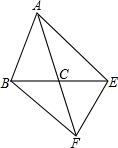 如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.
如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.
 如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.
如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.| A. | 90° | B. | 30° | C. | 60° | D. | 45° |
16.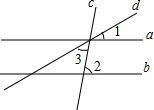 如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
 如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
如图,四条直线a,b,c,d.其中a∥b,∠1=30°,∠2=75°,则∠3等于( )| A. | 30° | B. | 40° | C. | 45° | D. | 75° |
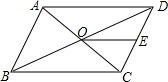 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为36cm,则△DOE周长是( )cm.
如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为36cm,则△DOE周长是( )cm. 在学完全等三角形后,李老师给出了下列题目:
在学完全等三角形后,李老师给出了下列题目: 如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.
如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.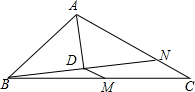 如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.
如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为3.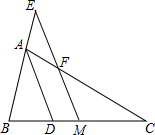 如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=$\frac{1}{2}$(AB+AC).
如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=$\frac{1}{2}$(AB+AC).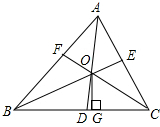 如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.
如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.