题目内容
9. 如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.
如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.
分析 根据平移的性质得到S△ABC=S△DEF,则利用S阴影部分+S△OEC=S梯形ABEO+S△OEC得到S阴影部分=S梯形ABEO,然后根据梯形的面积公式求解.
解答 解:∵△ABC沿BCC的方向平移到△DEF的位置,
∴S△ABC=S△DEF,
∴S阴影部分+S△OEC=S梯形ABEO+S△OEC,
∴S阴影部分=S梯形ABEO=$\frac{1}{2}$×(4+6)×3=15.
故答案为15.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.

练习册系列答案
相关题目
19.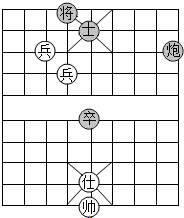 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )| A. | (8,7) | B. | (0,4) | C. | (0,0) | D. | (4,0) |
4.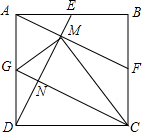 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
19. 如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
 如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )| A. | $\sqrt{6}$:2 | B. | 3:2 | C. | $\sqrt{5}$:3 | D. | 5:3 |
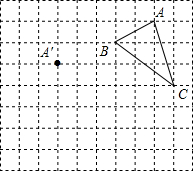 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点. 如图,已知AF∥CD,AB∥DE,那么∠A=∠D吗?请说明理由.
如图,已知AF∥CD,AB∥DE,那么∠A=∠D吗?请说明理由. 如图,
如图,