题目内容
18. 如图,
如图,(1)当直线MA∥NB时,试说明∠APB=∠MAP-∠NBP;
(2)若∠APB=∠MAP-∠NBP,则MA∥NB吗?请说明理由.
分析 (1)根据平行线的性质得出∠1=∠MAP,再由三角形外角的性质即可得出结论;
(2)由已知条件和三角形的外角性质证出∠1=∠MAP,即可得出结论.
解答 (1)证明: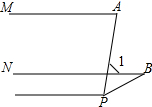 如图所示;
如图所示;
∵MA∥NB,
∴∠1=∠MAP,
又∵∠1=∠APB+∠NBP,
∴∠MAP=∠APB+∠NBP,
∴∠APB=∠MAP-∠NBP;
(2)解:MA∥NB;理由如下:
∵∠APB=∠MAP-∠NBP,∠1=∠APB+∠NBP,
∴∠1=∠MAP,
∴MA∥NB.
点评 本题考查了平行线的判定与性质、三角形的外角性质;解答此题的关键是熟练掌握平行线的性质及三角形内角与外角之间的关系.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.从长度分别是2,3,4的三条线段中随机抽出一条,与长为1,3的两条线段首尾顺次相接,能构成三角形的概率是( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 0 |
7.已知x=2是方程x2-a2=0的一个根,则a的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 4 |
 如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.
如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.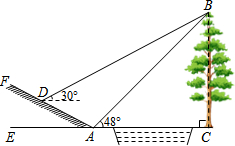 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡脚∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,$\sqrt{3}$≈1.7)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡脚∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,$\sqrt{3}$≈1.7) 如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.
如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.