题目内容
4.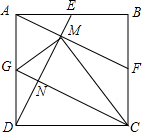 如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:
如图,正方形ABCD的三边中点E、F、G,连ED交AF于M,GC交DE于N,下列结论:①AF⊥DE;
②AF∥CG;
③CD=CM;
④∠CMD=∠AGM.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
分析 由△ADE≌△BAF得∠ADE=∠BAF,由此推出①正确;由四边形AGCF是平行四边形,推出②正确;可以证明CG是DM的垂直平分线,由此推出③正确;假设④成立推出∠AGM=60°,显然不可能,由此即可解决问题.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAC=∠ADC=∠DCB=∠B=90°,
∵AE=EB=AG=DG=BF=CF,
在△ADE和△ABF中,
$\left\{\begin{array}{l}{AE=BF}\\{∠DAE=∠B}\\{AD=AB}\end{array}\right.$,
∴△ADE≌△BAF,
∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AEM=90°,
∴∠AME=90°,
∴AF⊥DE,故①正确,
∵AG=CF,AG∥CF,
∴四边形AGCF是平行四边形,
∴AF∥CG,故②正确,
∵AF⊥DE,
∴CG⊥DM,
∵AG=GD,
∴GM=GD,
∴MN=DN,
∴CM=CD,故③正确,
若∠CMD=∠AGM,则∠AGM=∠CMD=2∠GMD,
∴∠GMD=30°,∠AGM=60°,
这个显然不可能,故④错误.
故选A.
点评 本题考查正方形的性质、全等三角形的判定和性质、平行四边形的判定和性质、线段垂直平分线的性质等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
15. 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
(1)a=35;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
12. 如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
 如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )| A. | 28° | B. | 34° | C. | 56° | D. | 68° |
14.已知m+2n=2,关于整式①m2+4n(m+n),②2n2+mn+m的值,下列说法正确的是( )
| A. | ①是常数,②不是常数 | B. | ①是不常数,②是常数 | ||
| C. | ①、②都是常数 | D. | ①、②都不是常数 |
 如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.
如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.