题目内容
20.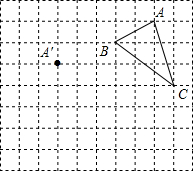 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′;
(2)若连接AA′,BB′,则AA′,BB′的数量和位置关系是平行且相等.
(3)作出BC边上的中线AD;
(4)求△ABD的面积.
分析 (1)直接利用点A变换为A′得出平移规律,进而得出答案;
(2)利用平移的性质得出AA′,BB′的数量和位置关系;
(3)利用网格得出BC的中点,进而得出答案;
(4)利用△ABD的面积=$\frac{1}{2}$S△ABC,进而得出答案.
解答 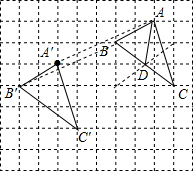 解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;
(2)AA′,BB′的数量和位置关系是:平行且相等;
故答案为:平行且相等;
(3)如图所示:AD即为所求;
(4)△ABD的面积=$\frac{1}{2}$S△ABC=$\frac{1}{2}$(9-1-1.5-3)=1.75.
点评 此题主要考查了平移变换以及三角形面积求法等知识,正确应用用平移的性质是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
15. 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
(1)a=35;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
12. 如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
 如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )
如图,AB∥CD,AC的垂直平分线分别交AC,BD于E,F,若∠C=56°,则∠BAF的度数是( )| A. | 28° | B. | 34° | C. | 56° | D. | 68° |
10.从长度分别是2,3,4的三条线段中随机抽出一条,与长为1,3的两条线段首尾顺次相接,能构成三角形的概率是( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 0 |
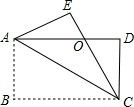 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形的面积. 如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.
如图,把直角三角形ABC沿BC方向平移到直角三角形DEF的位置,若AB=6,BE=3,GE=4,则图中阴影部分的面积是15.