题目内容
 如图,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.
如图,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.(1)已知
| 1 |
| m |
| 2 |
| m+2 |
(2)当
| AP |
| PB |
2-
| ||
2+
|
(3)在(1)的条件下,且
| AP |
| PB |
| 1 |
| 2 |
考点:圆的综合题
专题:
分析:(1)解关系式得出m的值,再利用m求出角的关系进而求出∠BCD、∠ACD的度数.
(2)由所给关系式结合直径求出AP,OP,据使弦CD最短,求出∠BCD、∠ACD的度数,即可求出m的值.
(3)连结AD、BD,先求出AD,BD,AP,BP的长度,利用△APC∽△DPB和△CPB∽△APD得出比例关系式,利用比例关系式结合勾股定理求出CP,PD,即可求出CD.
(2)由所给关系式结合直径求出AP,OP,据使弦CD最短,求出∠BCD、∠ACD的度数,即可求出m的值.
(3)连结AD、BD,先求出AD,BD,AP,BP的长度,利用△APC∽△DPB和△CPB∽△APD得出比例关系式,利用比例关系式结合勾股定理求出CP,PD,即可求出CD.
解答:解:(1)由
=
,
解得 m=2,
如图1,连结AD、BD.

∵AB是⊙O的直径
∴∠ACB=90°,∠ADB=90°
又∵∠BCD=2∠ACD,∠ACB=∠BCD+∠ACD
∴∠ACD=30°,∠BCD=60°
(2)如图2,连结OD.

∵
=
,AB=4,
∴
=
,则(2+
)AP=4(2-
)-(2-
)AP,
解得AP=2-
∴OP=2-AP=
要使CD最短,则CD⊥AB于P
∴cos∠POD=
=
,
∴∠POD=30°
∴∠ACD=15°,∠BCD=75°
∴∠BCD=5∠ACD
∴m=5,
故存在这样的m值,且m=5
(3)如图3,连结AD、BD.

由(1)可得∠ABD=∠ACD=30°,AB=4
∴AD=2,BD=2
,
∵
=
,
∴AP=
,BP=
,
∵∠APC=∠DPB,∠ACD=∠ABD
∴△APC∽△DPB
∴
=
=
,
∴AC•DP=AP•DB=
•2
=
①,
PC•DP=AP•BP=
•
=
②
同理△CPB∽△APD
∴
=
,
∴BC•DP=BP•AD=
•2=
③,
由①得AC=
,由③得BC=
∴AC:BC=
:
=
,
在△ABC中,AB=4,
∴(
)2+(
)2=42,
∴DP=
由②PC•DP=PC•
=
,得PC=
,
∴DC=CP+PD=
+
=
.
| 1 |
| m |
| 2 |
| m+2 |
解得 m=2,
如图1,连结AD、BD.

∵AB是⊙O的直径
∴∠ACB=90°,∠ADB=90°
又∵∠BCD=2∠ACD,∠ACB=∠BCD+∠ACD
∴∠ACD=30°,∠BCD=60°
(2)如图2,连结OD.

∵
| AP |
| PB |
2-
| ||
2+
|
∴
| AP |
| 4-AP |
2-
| ||
2+
|
| 3 |
| 3 |
| 3 |
解得AP=2-
| 3 |
∴OP=2-AP=
| 3 |
要使CD最短,则CD⊥AB于P
∴cos∠POD=
| OP |
| OD |
| ||
| 2 |
∴∠POD=30°
∴∠ACD=15°,∠BCD=75°
∴∠BCD=5∠ACD
∴m=5,
故存在这样的m值,且m=5
(3)如图3,连结AD、BD.

由(1)可得∠ABD=∠ACD=30°,AB=4
∴AD=2,BD=2
| 3 |
∵
| AP |
| PB |
| 1 |
| 2 |
∴AP=
| 4 |
| 3 |
| 8 |
| 3 |
∵∠APC=∠DPB,∠ACD=∠ABD
∴△APC∽△DPB
∴
| AC |
| DB |
| AP |
| DP |
| PC |
| BP |
∴AC•DP=AP•DB=
| 4 |
| 3 |
| 3 |
8
| ||
| 3 |
PC•DP=AP•BP=
| 2 |
| 3 |
| 8 |
| 3 |
| 16 |
| 9 |
同理△CPB∽△APD
∴
| BP |
| DP |
| BC |
| AD |
∴BC•DP=BP•AD=
| 8 |
| 3 |
| 16 |
| 3 |
由①得AC=
8
| ||
| 3DP |
| 16 |
| 3DP |
∴AC:BC=
8
| ||
| 3 |
| 16 |
| 3 |
| ||
| 2 |
在△ABC中,AB=4,
∴(
8
| ||
| 3DP |
| 16 |
| 3DP |
∴DP=
2
| ||
| 3 |
由②PC•DP=PC•
2
| ||
| 3 |
| 16 |
| 9 |
8
| ||
| 21 |
∴DC=CP+PD=
8
| ||
| 21 |
2
| ||
| 3 |
22
| ||
| 21 |
点评:本题主要考查了圆的综合题,解题的关键是在圆中结合三角形相似得出比例关系式,运用比例关系式求出比段之间的关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
| A、(4,5) |
| B、(5,4) |
| C、(5、4) |
| D、(4、5) |
 在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.
在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A. 在平面直角坐标系xOy中,点M(
在平面直角坐标系xOy中,点M(
 如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B. 已知数a,b在数轴上的位置如图,化简
已知数a,b在数轴上的位置如图,化简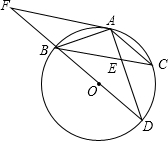 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.